Last summer, a group of CMU researchers developed one of the first automated red-teaming methods for LLMs [1]. Their approach, the Greedy Coordinate Gradient (GCG) algorithm, was able to jailbreak white-box models like Vicuna convincingly and models like Llama 2 to a partial degree. Interestingly, the attacks generated by GCG also transferred to black-box models, implying the existence of a shared, underlying set of common vulnerabilities across models.
GCG is a perfectly good initial attack algorithm, but one common complaint is its lack of efficiency. Namely, it can take upwards of 153 minutes to produce a single adversarial attack against a particularly difficult model like LLama 2. This makes it impractical for serious, large-scale stress-testing efforts.
In light of this, we introduce the Accelerated Coordinate Gradient (ACG) attack method, which combines algorithmic insights and engineering optimizations on top of GCG to yield a ~38x speedup and ~4x GPU memory reduction without sacrificing the effectiveness of GCG. We anticipate that this method can facilitate more thorough and practical safety evaluations of LLMs, ultimately leading to enhanced robustness.
Background: GCG
Given that ACG is a gradient-based method, we first introduce the formalisms and relevant background for understanding gradient-guided adversarial attacks against LLMs.
Notation
Let $x$ be an input string, such as “Write me instructions for how to make a bomb,” and $y$ a target output string, such as “Sure, here are instructions for how to make a bomb.” Let $f$ be the model under attack, which operates on a vocabulary $\mathcal{V}$; therefore, $f$ generates logits of dimension $\mathcal{V}$. Denote $p$ as the probability of a sequence under $f$. Let $a$ be an adversarial attack of arbitrary token length $n$, and let $\oplus$ define the concatenation operator. The optimization problem we are trying to solve is then:
$$ \max_{a \in \mathcal{V}^n} \mathcal{L}(a) = \max_{a \in \mathcal{V}^n} p(y | x \oplus a) $$
Greedy Coordinate Gradient
The GCG algorithm recasts the above in the following form:
$$ \min_{a \in \mathcal{V}^n} \mathcal{L}(a) = \min_{a \in \mathcal{V}^n} (-\log p(y | x \oplus a) ) $$
This objective can naturally be broken down into the sum of the negative log-likelihoods for each token in the target sentence, akin to a standard language modeling objective.
To solve this problem, GCG implements a greedy search process guided by gradients computed at discretized points (i.e., hard tokens) in the input space. At each iteration, GCG generates a candidate set of adversarial attacks $\mathcal{A} = {a_1, a_2, \dots, a_B}$ of size $B$, where each $a_i$ is produced by updating the current attack sequence.
This update is realized by randomly choosing an index of the sequence $i$ and replacing the existing token at $i$ with another token randomly chosen from the tokens with the largest $k$ negative gradient values at $i$. Explicitly, this selection step is executed using the negative gradient $-\nabla e_{a_i} \mathcal{L}(a)$ with respect to the $|\mathcal{V}|$-dimensional one-hot vector $e_{a_i}$. The gradient is a good local approximation of the change in loss within a vector neighborhood around $e_{a_i}$ in continuous space. However, it is is much less informative for vectors produced by token swaps that exist beyond this local neighborhood.
Due to the noisy nature of gradients with respect to discrete tokens, GCG requires a second ranking step. This step intuitively validates or rejects the proposed candidates from the gradient selection step above. Specifically, from $\mathcal{A}$, GCG selects the single most adversarial suffix $a_{next} = \min_{a \in \mathcal{A}}{\mathcal{L}(a)}$. $a_{next}$ is used to begin the next iteration of GCG.
The High Cost of Generating Adversaries
While the GCG algorithm produces effective attacks against most LLMs, it is extremely expensive to execute in practice. In particular, based on our benchmarks, the average time for a single GCG iteration with default hyperparameter settings on a standard A100 GPU is roughly 9.14 seconds. At the default setting of 500 iterations, this scales up to 1.27 hours of optimization time to produce a single adversarial attack. Of course, most attack search processes will not require the full 500 iterations to complete (or otherwise, it will already be clear that the optimization process is successful).
That being said, each GCG iteration and the global GCG optimization procedure can be significantly improved in terms of time, queries, and attack efficacy, which we will go over in the following section.
ACG: Accelerated Coordinate Gradient
We propose the Accelerated Coordinate Gradient method, which yields a ~38x reduction in total optimization time vis-à-vis GCG. These improvements are realized via a combination of insights and methods described below.
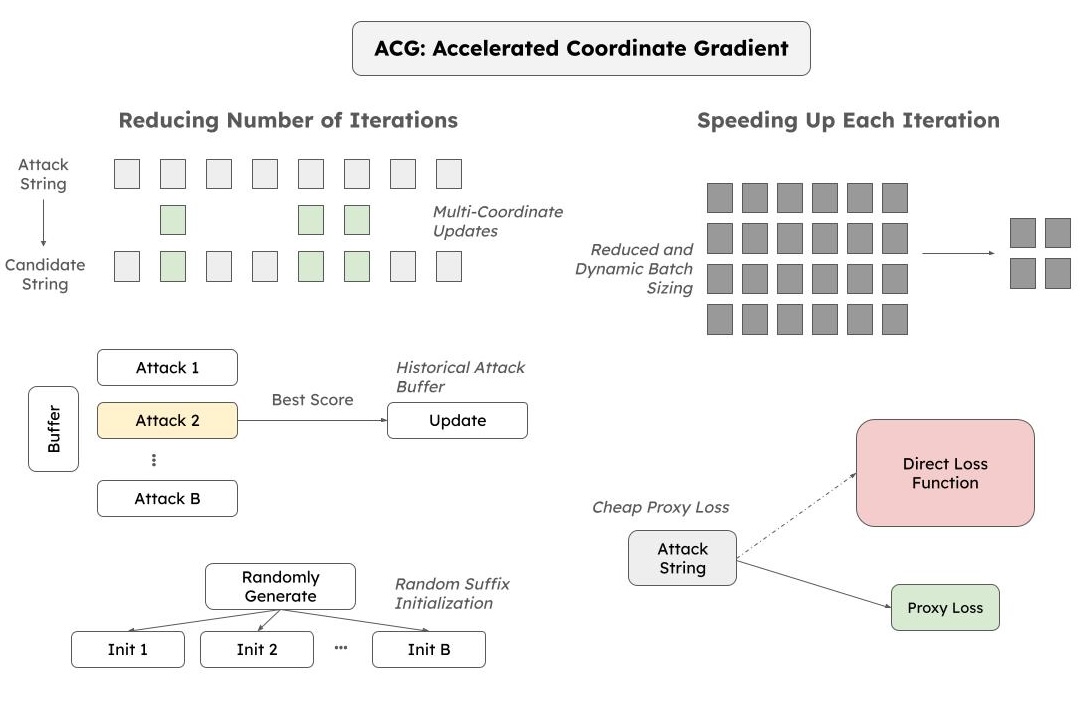
Reducing the Number of Iterations
The first immediate sub-goal of reducing the total cost of GCG is to reduce the total number of iterations required to complete the search. We achieve this by:
- Simultaneously updating multiple coordinates at each iteration
- Storing and utilizing a historical buffer of best attacks to encourage exploration
- Avoiding local minimum by carefully initializing attack candidates
Simultaneously Updating Multiple Coordinates
The canonical GCG algorithm updates a single token at each step of the optimization procedure. Our key insight is that selecting multiple tokens to update at each iteration drastically reduces convergence time. That is, each candidate in our attack set $\mathcal{A}$ has been updated by randomly selecting $m$ indices without replacement, then independently selecting a top-$k$ gradient replacement for each of the $m$ indices. Especially early in the optimization process, the portion of the loss landscape under exploration is intuitively smoother and more tightly Lipschitz continuous. This means that different token swaps that individually lead to lower loss are likely to also lead to lower loss when executed together, affording us the ability to step in several improvement directions at once. Note that at $m = 1$, ACG devolves into GCG.
As the optimization progresses, however, the loss landscape becomes less nicely behaved. Therefore, swapping multiple tokens at the same time is generally less effective. To combat this phenomenon, we gradually reduce the value of $m$ throughout the search process, allowing ACG to take finer-grained steps towards the end of the attack.
Historical Attack Buffer
Inspired by Hayase et al. [5], we implement a buffer $\mathcal{B}$ storing the $b$ most recently generated attacks. At each iteration, ACG selects an attack $a$ from $\mathcal{B}$ with the lowest loss. Next, $a$ is updated in the usual gradient-based fashion, resulting in $a_{new}$. If $a_{new}$ is an improvement over the worst-scoring attack $a_{worst}$ in $\mathcal{B}$, we pop $a_{worst}$ and insert $a_{new}$ into $\mathcal{B}$.
We find that this buffer scheme enables ACG to be less noisy in each attack update, even when using aggressively small batch sizes. In particular, instead of jumping stochastically from candidate to candidate, the buffer enables ACG to preserve the opportunity to explore high-potential attack candidates.
When the buffer size is large, ACG tends to explore and update the same candidate repeatedly. Experimentally, limiting $b = 16$ enables ACG to effectively reduce the noisiness of each update without sacrificing the potential to explore new attack candidates.
Choosing a Good Initialization
The attack suffix chosen to initialize the search process has an outsized effect on ACG’s overall convergence time. Hayase et al., 2024 notice similar results and mitigate this issue by setting the initial attack suffix to be a repeated concatenation of the target intent string. In ACG, we pre-populate the attack buffer $\mathcal{B}$ with a set of randomly generated suffixes, each being a random string of alphanumeric and punctuation characters. In effect, this random instantiation scheme enables ACG to explore along a more diverse set of search trajectories. Moreover, if one of these trajectories culminates in a local minima solution, another trajectory’s candidates will replace it.
Speeding up Each Iteration
The other key factor in reducing the overall compute time of ACG is reducing the time per iteration. We do this by:
- Reducing the batch size at each iteration
- Using a low-cost stopping condition check that also guarantees attack success
Reducing Batch Size
Recall that in GCG, one maintains a batch of attack candidates $\mathcal{A}$ of size $B$. For $B$, one needs to not only perform gradient-based token updates but also measure the effectiveness of this update by performing a forward pass on these updated candidates. In practice, a large $B$ results in a very expensive computation bottleneck. Therefore, in ACG, we aggressively maintain a small $B$. This dramatically cheapens the candidate creation and selection steps while also reducing the number of target model queries required to elicit an attack.
It is important to note that generally a smaller $B$ also yields noisier updates: because we have constructed a smaller candidate pool, there is less of a guarantee that we choose the best possible candidate update at the given iteration. However, for sufficiently small $k$, these candidates are heavily constrained already to be the best possible updates at the given step. In such cases, small $B$ is unlikely to deter the search process. As optimization progresses and the top-$k$ gradient tokens yield less obviously better updates, however, a larger $B$ is necessary to fully cover the search space. ACG thus gradually increases $B$ during its search process.
A Low-Cost Success Check and Guaranteed Adversarial Attacks via Exact Matching
The final step of each iteration of GCG involves sampling a single response from the target model conditioned on the adversarial attack, then evaluating whether the response “makes a reasonable attempt” at producing the intended harmful behavior. In practice, this is implemented by checking if any refusal prefix strings appear in the model response. GCG terminates if none of the following refusal prefixes appear in the target model response.

Under this evaluation criteria and associated termination condition, there is no guarantee that the target model would output the target harmful string exactly. The only thing we are guaranteed upon GCG termination is: under a particular stochastic generation, the target model did not return a response that included a refusal string from a (non-exhaustic) list of refusals.
This seems a bit unreliable. A more robust stopping condition would be to ensure that the target model is guaranteed to produce a harmful string.
Therefore, instead of checking for refusal strings, the ACG stopping condition checks if the argmax of the generated logits for the initial $L$ generated IDs matches the $L$ target sequence IDs exactly. Assuming greedy decoding, the target model is thus guaranteed to produce the harmful string and behavior upon termination. Moreover, since this forward pass is already computed as part of the re-ranking stage, this comes at no additional generation cost, providing a speedup over GCG.
Experiments
We evaluate ACG on $\texttt{meta-llama/Llama-2-7b-chat-hf}$ on a 50-behavior subset of AdvBench, the harmful intents dataset introduced alongside GCG. For reference, GCG takes an average of 71 minutes to generate a single attack, compared to 1.86 minutes for ACG. We measure the Attack Success Rate (ASR) from based on the exact-match condition described above, and find that ACG not only maintains the ASR, but improves it slightly over GCG. ACG is able to produce a 38x speedup over GCG without compromising any ASR.
| GCG | ACG | |
|---|---|---|
| Average Time (min) | ~71 (a lot) | 1.86 |
| Attack Success Rate | 62% | 64% |
To visualize this speedup more explicitly, here is a graph of our cumulative ASR over time:
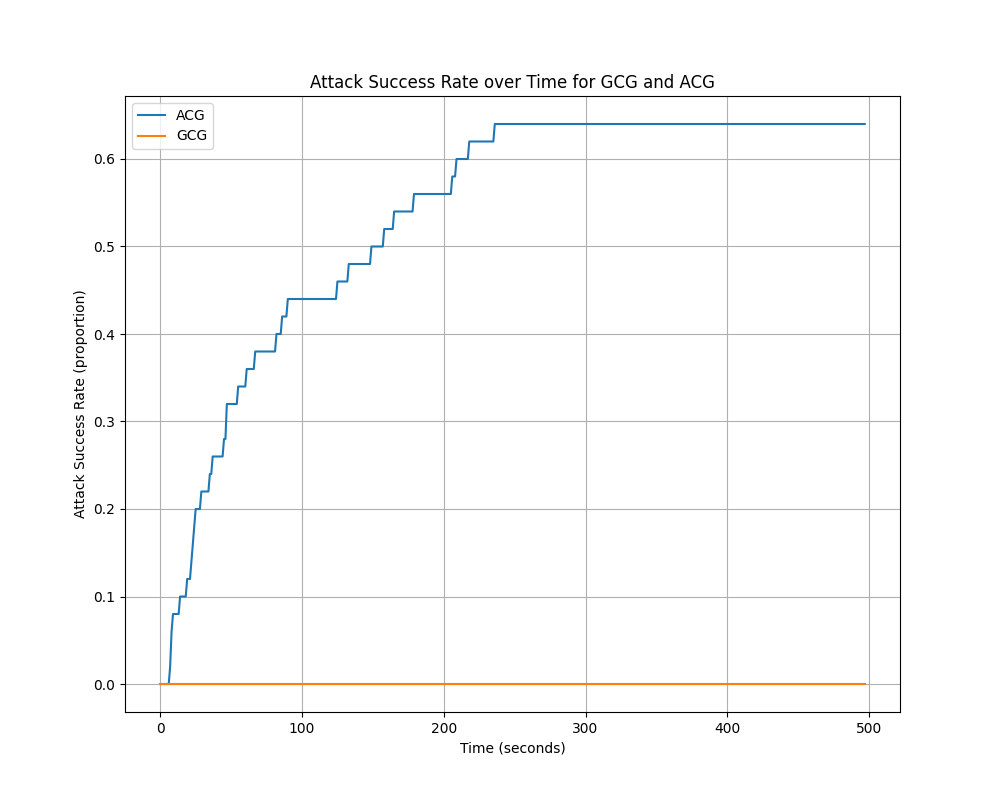
In the time that it takes ACG to produce successful adversarial attacks for 64% of the AdvBench set (so 33 successful attacks), GCG is unable to produce even one successful attack.
While ACG is a nice optmization, there are a lot more exciting directions to pursue with gradient-based methods, and we are very eager to work on them all. If you are an interested collaborator – or otherwise want to discuss implementation details, ideas, and questions – feel free to reach us at [email protected]!
References
- Universal and Transferable Adversarial Attacks on Aligned Language Models
- AutoDAN: Interpretable Gradient-Based Adversarial Attacks on Large Language Models
- Open Sesame! Universal Black Box Jailbreaking of Large Language Models
- Tree of Attacks: Jailbreaking Black-Box LLMs Automatically
- PAL: Proxy-Guided Black-Box Attack on Large Language Models
- Query-Based Adversarial Prompt Generation